Our group takes on and explores emerging and challenging problems that intrigue us, in collaboration with other researchers at the University of Tennessee and other universities and laboratories. For example, we are employing machine learning for developing surrogate (low-fidelity) models that complement physics-based (high-fidelity) models to accelerate analyses of problems for calibration, validation, and uncertainty quantification. Historically, we have looked at other topics including: Fast Fourier Transform based modeling of material microstructures, mixture theory for modeling growth in biological tissues, estimation of discretization error in (and thus accuracy of) nonlinear finite element models of materials, and deriving stable and efficient formulations for linear tetrahedral finite element models. These topics don’t exactly fit in the other two themes, but they have intrigued us, and one day may lead to an additional research theme for our group.
Current Project
Creep refers to the slow deformation of a material during sustained stress and high temperature. Such environments are common in the components and tubing of power plants, as an example. Creep experiments on ferritic-martensitic steels typically exhibit a moderate amount of scatter in time to rupture. Computational modeling is being pursued to understand potential sources for this uncertainty (manufacturing process tolerance, material heterogeneity, …) to improve confidence in extrapolation of creep life to operating conditions and time horizons. Also, these physics-based microstructural models contain ten to twenty material parameters, and the manual calibration of the material parameters for novel yet related alloy systems is time consuming. Thus, these related problems of parameter sensitivity and uncertainty propagation are being approached in our group using machine learning surrogate models for acceleration and state-of-the-art analysis formulations such as Polynomial Chaos Expansion and Gaussian Process Regression.
Sponsorship: Oak Ridge National Laboratory
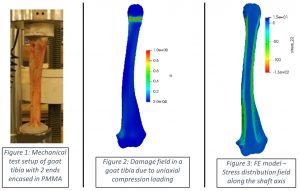
This study aims to develop a physics-based (PB) model that can assess the effect of unicortical defects on the goat tibia with lessened requirement for experimenting with cadaver specimens or live animals. The work flow requires building a finite element (FE) model and calibrating it to create a digital twin of the goat tibia. The calibration process started with the DICOM images received from the CT scanner of the goat tibia and phantom tubes, which were used for density calibration. Several open source software, utilization of which is one of the novelties of this work, were used to calibrate the model. After validating the elastic model, simulation was done with phase-field model for capturing where cracking initiates in relation to the defect. In this step, the analysis for compression loading on intact tibiae will produce a simulated stress distribution and crack profile at failure to be matched against laboratory testing of the same 2 specimens. The PB phase field fracture model is expected to serve as a virtual laboratory for tibiae behavior of similar age and quality subjected to compression loading, predicting failure load and crack location with 85% accuracy. The project has led the understanding and development of a novel work flow to build an ovine FE model that has the potential of aiding in fracture healing enhancement, implant design and insertion types, and shortening time to full function recovery.
Sponsorship: UT Seed Grant: One Health Initiative
Past Projects

Examples of models of nearly incompressible materials (e.g. particle-filled rubber) meshed with linear tetrahedral elements and undergoing large deformations
Adding reinforcing particles to materials such as elastomers and plastics enhances mechanical properties, including toughness, conductivity, and stiffness, and may also produce emergent functionality if properly designed. Computational modeling of such heterogeneous materials often requires the use of tetrahedral finite elements due to the existence of robust mesh generators that can resolve the complex geometric features. However, traditionally linear tetrahedral elements produce poor-quality solutions except on extremely-refined meshes due to locking and other pathologies. Therefore, we developed a stabilized low-order tetrahedral element for modeling incompressible materials undergoing large deformations that is free from numerical tunable parameters.
Sponsorship: National Science Foundation
Finite element models are approximations of mathematical models of reality; the former possesses discretization error (insufficient mesh resolution, …) and the latter possesses modeling error (inaccurate constitutive models, …). Having an estimate on the amount and distribution of these errors in a simulation provides confidence in applying the results to real designs. The Variational Multiscale (VMS) paradigm centers on the coarse and fine scales present in numerical approximations of mathematical models and has been applied to derive stabilized methods, error estimation approaches, and other numerical approaches. This project studies the efficacy of fine-scale models in the VMS method to estimate the error in finite element solutions so as to quantify the global and/or local level of accuracy and identify zones where mesh refinement is needed. We focus on mixed elasticity, interfaces, and nonlinear problems.
Sponsorship: National Science Foundation